こんにちは。TDSCの高橋です。
子供のころ、けん玉にずいぶんハマっていた時期がありました。
玉を乗せたり刺したりもそうですが、何よりけん(持ち手の部分のこと)と玉がヒモで括りつけられているのをいいことに、思いっきり玉を振り回してよく怒られていました。
そういえば、ビー玉にテープで毛糸をくっつけて、振り回して怒られたことも。
振り回すのが好きだったのかもしれません。
今の僕にもちょっとだけわかる気がします。
人工衛星は地球の周りを回っています。けんの周りを回る玉のように、地球を中心とした円や楕円を描きます。
では、人工衛星は何を使って回っているのでしょうか。
衛星の回る原理 – パワーの源は、”地球”
衛星はどうやって回っているのだろうか?

そもそも静止軌道衛星に限らず、人工衛星が地球の周りを回ることができるのはなぜなのか。
地球の周り、すなわち宇宙を移動しているわけですから、パッと思いつくのはロケットなどのように燃料を燃やす推進装置ですよね。
宇宙での移動手段と言えば、ガ〇ダムやス〇ーウォーズなどのSF作品でもよく見かけるロケット噴射を想像してしまいます。
でも、あまり人工衛星からロケットに火を噴いている図は思い浮かびません…。
話は少し変わりますが、人工衛星の寿命は殆どの場合「燃料」によって決まります。
衛星が力尽きるその時は、その「燃料」が空っぽになったときともいうことができます。
衛星の打ち上げには、設計や製作、打ち上げそのもの…と膨大な費用が掛かるため、できれば長い寿命であった方がコストを抑えることができます。
しかし、衛星に燃料を積めば積むほど重くなるため、その分コストが高くなる、そもそも打ち上げるロケットのパワーが足りない、という本末転倒な事態になってしまいます。
つまり、衛星にとって「燃料」とは命そのものといっても過言ではありません。
単純に噴射するだけではただまっすぐに進んでしまいますから、地球の周りを丸く(円形に)回るためには姿勢制御で更に燃料を使ってしまうことが想像できます。

宇宙にも及ぼす大きなチカラ – 万有引力
そこで登場するのが、”地球の持つパワー”です。
これを利用することで、人工衛星は燃料を必要最低限に抑えることができます。
(ちなみに、燃料は細かい姿勢制御や、軌道を修正する際などに使われます。)
その”地球のパワー”の正体は、『万有引力』…つまり地球の重力です。
宇宙に飛び出た人工衛星ですが、重力圏…地球が重力を及ぼす範囲からは脱していません。
そのため、衛星は地球上にいる我々と同じように重力を受けることになります。そうすると一見、重力に引かれて地球へ真っ逆さまになりそうですが…?
第一宇宙速度
投げても落ちないボール?
『第一宇宙速度』。
宇宙に詳しくなくとも、どこかで聞いたことはある…という言葉かもしれません。
その『第一宇宙速度』は、人工衛星と密接に関係しています。
地球でボールを投げると、放物線を描いて落ちてきます。
それは、地球の重力がボールに働いているからですが、もしボールを投げる強さ…つまり速度を早くしていくと仮定すると、ボールの飛距離は段々遠くなっていきます。
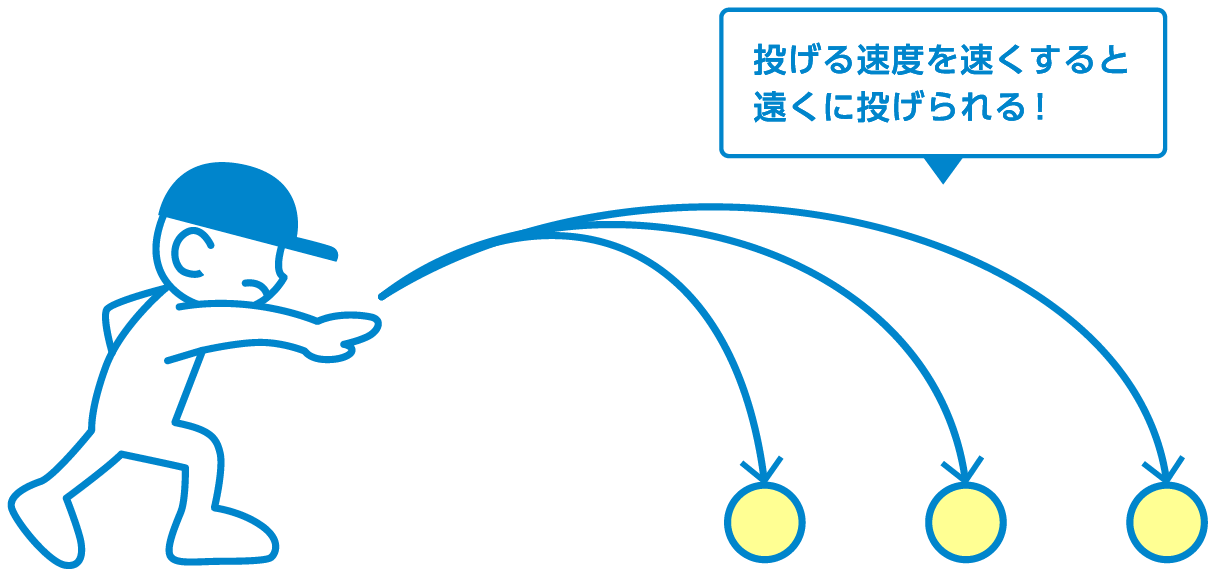
地球は平坦ではなく概ね球体ですから、際限なくボールを投げる速さ(=初速)を上げていくと、最後には投げた人の場所に戻ってきます。
戻ってきたまま、地球の周りを回り続ける速度…それを『第一宇宙速度』と言います(正確には、地球は空気抵抗などによる影響があり一定の速度では進み続けない。そのため、重力のみを考慮しボールは減速しないと仮定する)。

この第一宇宙速度は基本的に地面すれすれ…(本来はあり得ませんが)地面0mを飛んでいることを仮定します。
それでは、地球から100km~36,000km以上を飛ぶ人工衛星の場合ではどうでしょうか。
大気のない(=空気抵抗のない)宇宙では、仮定ではなく実際に初速から減速することがありません。
つまり、ロケットから投げ出された速度のまま回り続けることができるため、地球に落ちることなく一周することができます。
その為、人工衛星を打ち上げる際には、第一宇宙速度に到達できるよう計算されているのです。
万有引力とのつり合い
第一宇宙速度に到達した人工衛星は、そのまま宇宙に飛び出してゆくのではなく、地球の重力圏にとらわれることになります。
しかし、十分な速度を持っているため地球に墜落せず、地球の周りを楕円形、若しくは円形に周回することになります。
その際人工衛星に働いている力は下図のようになります。

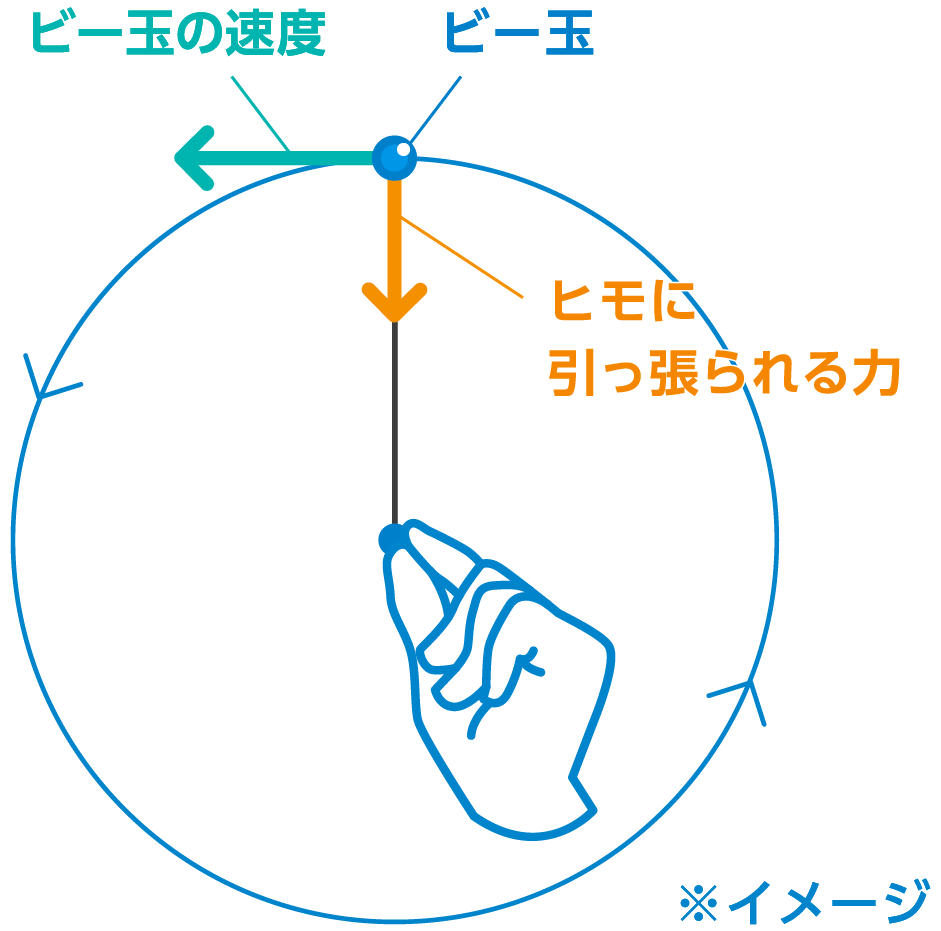
ヒモの先にビー玉を付け、手でつまんでくるくると回すと、ビー玉はヒモに引かれるため、飛び出さずにつまんだ部分を中心とした円形に周回します。
それと同じで、重力という見えないヒモに括りつけられた人工衛星は、外に飛び出していくことなく、地球の周りを回ることができるのです。
ちょこっとコラム : 向心力
人工衛星やビー玉に働く中心方向の力を向心力と呼びます。
また、向心力と全く同じ大きさで真逆方向の力を遠心力と呼びます。
この二つが釣り合うことで、人工衛星やビー玉は等速円運動(円周上を一定の速さで動く)をすることができます。
人工衛星の場合、向心力は重力(地球からの万有引力)です。
向心力と遠心力が釣り合わない場合、大きい方に人工衛星は飛び出してしまいます。
人工衛星が楕円ではなく円形に回る場合は等速円運動をしなければならないため、向心力と遠心力は釣り合います
実際に衛星の速度を計算してみよう!
静止軌道衛星の速度を計算してみる
ここまで、重力(万有引力)とロケットから飛び出した際の初速を利用して人工衛星が地球の周りを周回していること、そしてその初速には、『第一宇宙速度』という地球へ落ちてこない速度である必要があることをご説明いたしました。
では、実際に人工衛星はどのような速度を持っていれば地球へ落ちてこない軌道に乗ることができるのでしょうか。
ここでは静止軌道衛星を例にして計算してみます。
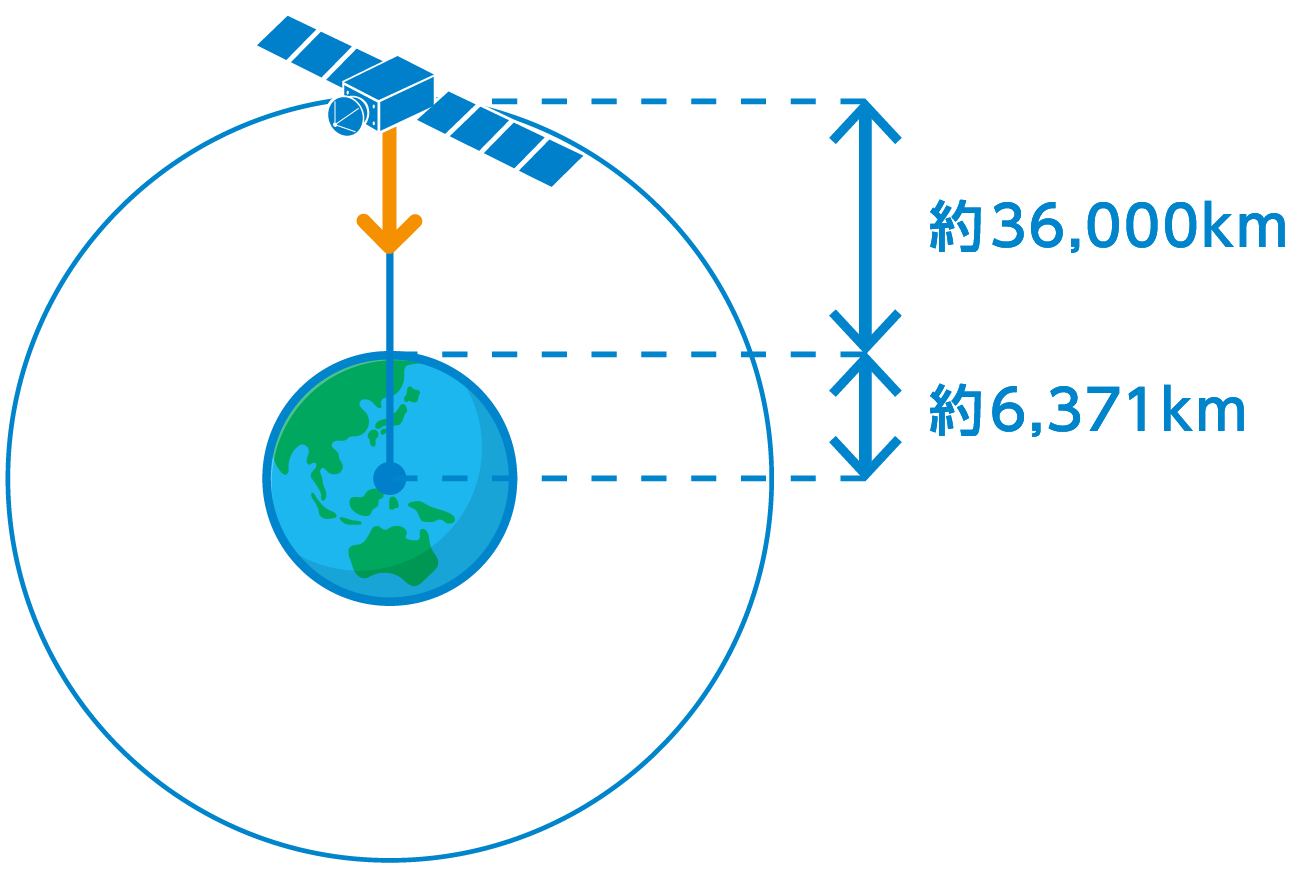
静止軌道衛星は地上から約の高さを周回しています。
また、地球の半径はですから、つまり人工衛星は地球の中心から約の高さを周回していることになります。
静止軌道衛星は等速円運動をしていますので、これを運動方程式に当てはめます。
- は人工衛星にかかる力、つまり万有引力
※ は万有引力定数、は地球の重さ、は距離 - は運動している物体の質量、つまり人工衛星の重さ
- は加速度、ここでは等速円運動では向心加速度。速度で求める。
※ 等速円運動では、中心に向かう加速度が発生しているため、常に向きを変えながら周回します。
その加速度を、向心加速度と呼びます。
実際に運動方程式に当てはめてみると、
左辺右辺を入れ替えて
ということになります。
万有引力定数、地球の質量の積を地心重力定数と呼びます。
地心重力定数は現在とされているため(単位を揃えるためにをに直します)
すなわち、約 つまり約 であることが分かります。
よって、静止軌道衛星(地上約)の場合、約 の初速があれば、地球の周りを周回する軌道に乗ることができる、ということになります。
ここで出てきた に着目すると、
になります。
地心重力定数、地球の半径は定数(場合によって変わる数値ではない)ことから、人工衛星の速度は人工衛星の高さによってのみ変動することが分かります。
ちょこっとコラム : 静止軌道衛星と速度
静止軌道衛星は地球と同じ周期(=24時間)で地球を一周することで、地上から見ると常に同じ一点にあることが特徴です。
そのメリットは常に同じ方向にアンテナを固定できる、等様々ですが、地球と同じ周期であることが最も重要です。
先ほど計算した通り、地上から約(つまり地球中心から)を円軌道で周回する場合の速度は必ず約になります。
24時間で地球の周りを回るということは、を24時間で回る必要があります。
『』
『』を組み合わせることで、
『24時間で1周りし、かつ人工衛星が重力で引っ張られず落ちない』
そんな人工衛星の高さが、地上から約、というわけなんです!
まとめ – 人工衛星は地球に振り回されている
今回は人工衛星がどのような力を使って地球の周りを回っているのかをご紹介しました。
燃料は細かい姿勢制御などあくまでサブであり、恒常的に人工衛星が回るための力の正体は地球が人工衛星に及ぼす万有引力がメインです。
また、そもそも宇宙に飛び出した後、万有引力と遠心力が釣り合う状態になる(再び地上に落ちてこない)ために、第一宇宙速度と呼ばれる速度でロケットから飛び出すことも必要です。
地球からの万有引力というヒモに括りつけられた人工衛星は、その燃料が尽き仕事を終えるまで、ビー玉のように振り回され続けているのです。